Day2.长度最小子数组、螺旋矩阵II
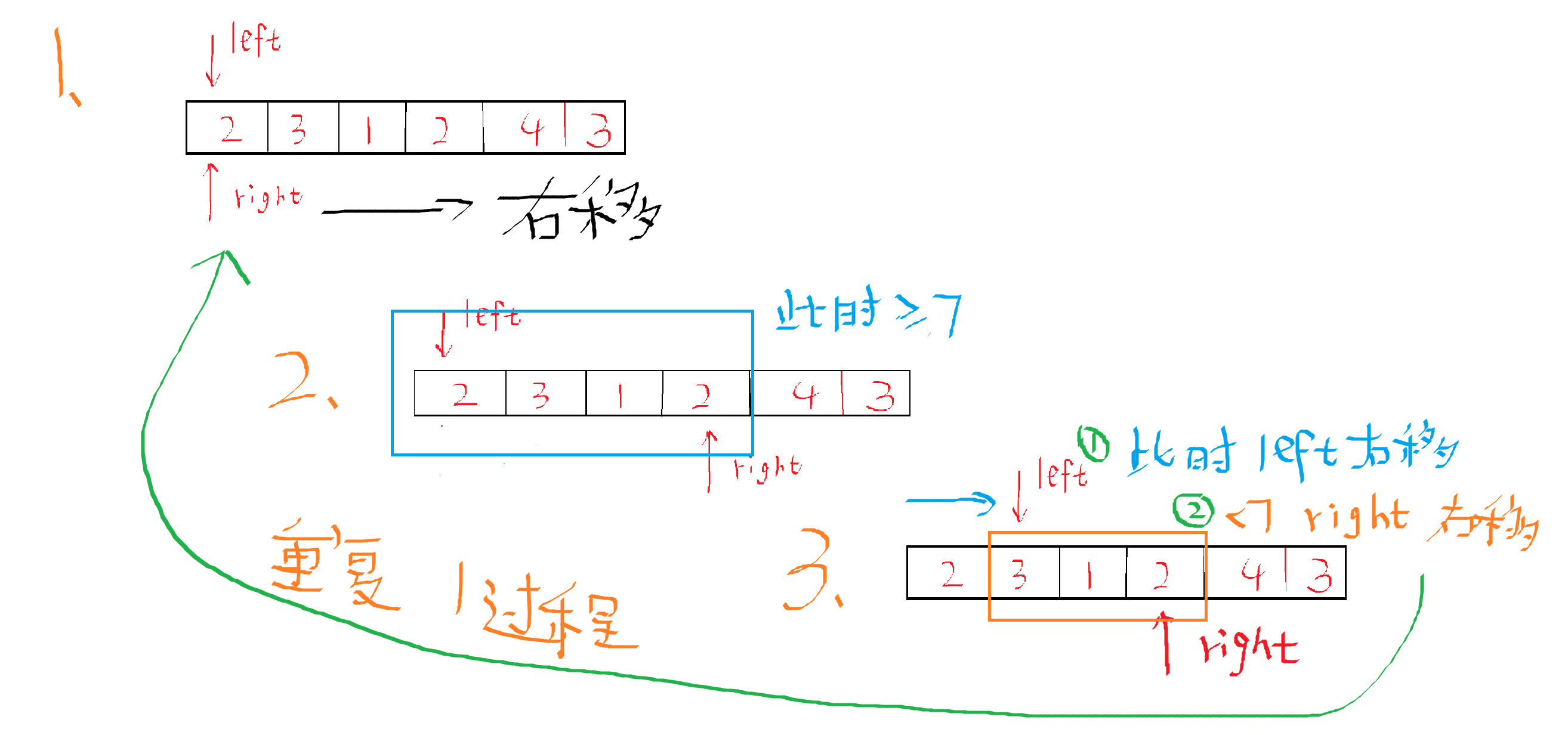
主要思路:一个数组,左右指针同时在起点,右指针不断向右移动,直到左右指针内sum和>=target,并且记录下当前长度,这个时候收缩left值,直到小于target,又重复右指针向右移动的过程,子数组长度只会在多次比较中保留最小的。
public static int minSubArrayLen(int s, int[] nums) {
//设置初始值,假如不存在就返回这个期望值。
int result = Integer.MAX_VALUE;//如果是0的话,后面更新result的时候永远是最小值0
//要获取总和>=target的最小长度的子数组,数组是连续的,我们可以把所有可能的情况全部枚举出来再筛选最小值
//但是这样时间复杂度是O(n^2),如果用滑动窗口做,时间复杂度是O(n)
int left = 0;
int right = 0;
int sum = 0;
//左右边界初始都在0位置,然后右边界一直向右,直到到达数组边界
// 如果窗口内的元素和>=target,左边界向右移动,缩小窗口,直到窗口内的元素和sum<target,记录下长度给result
// 然后右边界向右移动,直到窗口内的元素和>=target,再重复上面缩小窗口的步骤
while (right < nums.length) {
sum += nums[right];
//【内层循环】如果大于target了就开始缩小窗口
while(sum >= s){
//更新result值
result = Math.min(result, right - left + 1);
//向右缩小窗口,重新算sum,指针右移
sum -= nums[left];
left++;
}
//如果不大于target,就让right继续右移,直到边界
right++;
}
return result == Integer.MAX_VALUE ? 0 : result;
}这道题难点在于如何控制循环方向以及循环次数,并且需要注意n为奇偶数的时候的差异。
注意[][]分别对应[行][列],通过while控制结束条件,在里面写运动过程,可以拆分成”右滑、下滑、左滑、上滑“的运动过程。
n为偶数的时候是可以走完的,但是n为奇数的时候,中心永远有个格子是走不到的,这个时候可以手动控制移动的坐标,赋值拿到。
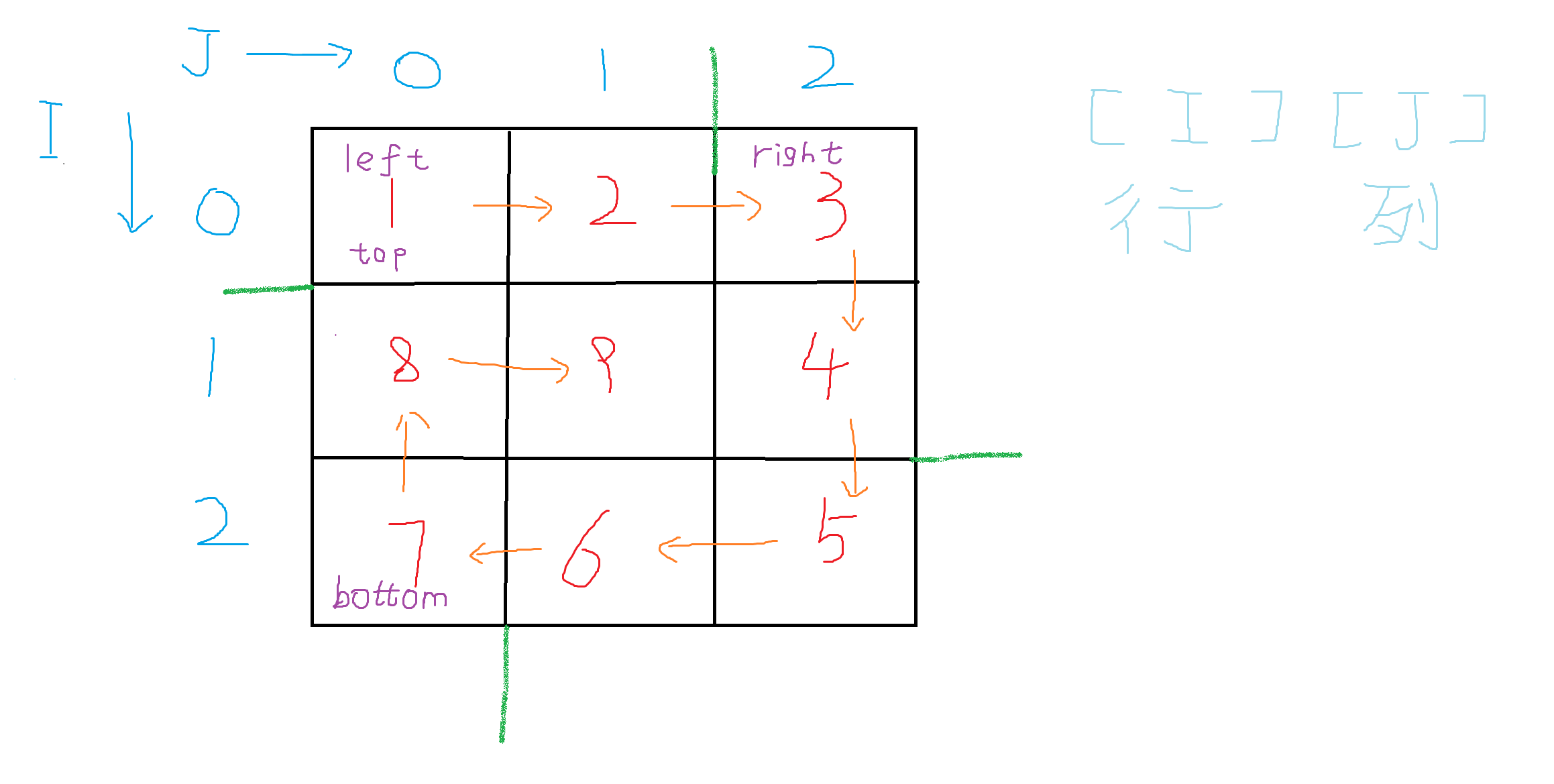
上述思路代码如下(优化版本在下方贴出):
public class Solution {
public int[][] generateMatrix(int n) {
//先定义一个二维数组,大小就是n
int result[][] = new int[n][n];
//区间,左闭右开,[ ) ,需要定义边界
int left = 0;
int right = n - 1;
int top = 0;
int bottom = n - 1;
//定义一个计数器,从1开始,如果计数器等于n^2,则返回结果
int count = 1;
//开始循环
while (left <= right && top <= bottom){
//从左往右走,行不动,列动
for (int i=left;i<right;i++){
result[top][i] = count;
count++;
}
//从上往下走,列不动,行动
for (int i=top;i<bottom;i++){
result[i][right] = count;
count++;
}
//从右往左走,行不动,列动
for (int i=right;i>left;i--){
result[bottom][i] = count;
count++;
}
//从下往上走,列不动,行动
for (int i=bottom;i>top;i--){
result[i][left] = count;
count++;
}
//假如有多个圈圈,现在走完了最外圈,需要处理边界了
//如果是奇数情况,中间永远会有一个格子跑不进去,所以需要提前边界处理
if (left == right && top == bottom){
result[top][left] = count;
return result;
}
left++;
right--;
top++;
bottom--;
}
return result;
}
}优化版本
//优化后
public class Solution {
public int[][] generateMatrix(int n) {
int[][] result = new int[n][n];
int left = 0, right = n - 1, top = 0, bottom = n - 1;
int num = 1;
//对于正方形矩阵,left <= right 和 top <= bottom 是等价的
// while (left <= right && top <= bottom) 可以简化为 while (left <= right)
while (left <= right) {
// 处理奇数情况的中心点
if (left == right) {
result[top][left] = num;
break;
}
// 从左到右
for (int i = left; i < right; i++) result[top][i] = num++;
// 从上到下
for (int i = top; i < bottom; i++) result[i][right] = num++;
// 从右到左
for (int i = right; i > left; i--) result[bottom][i] = num++;
// 从下到上
for (int i = bottom; i > top; i--) result[i][left] = num++;
// 缩小边界
left++;
right--;
top++;
bottom--;
}
return result;
}
}数组的概念是:在连续内存空间上存储相同类型数据的集合。
特点:1.下标从0开始。2.内存空间的地址连续(因此查询快,增删尾节点O1,增删头节点On)。3.数组元素实际不是删除,而是覆盖。
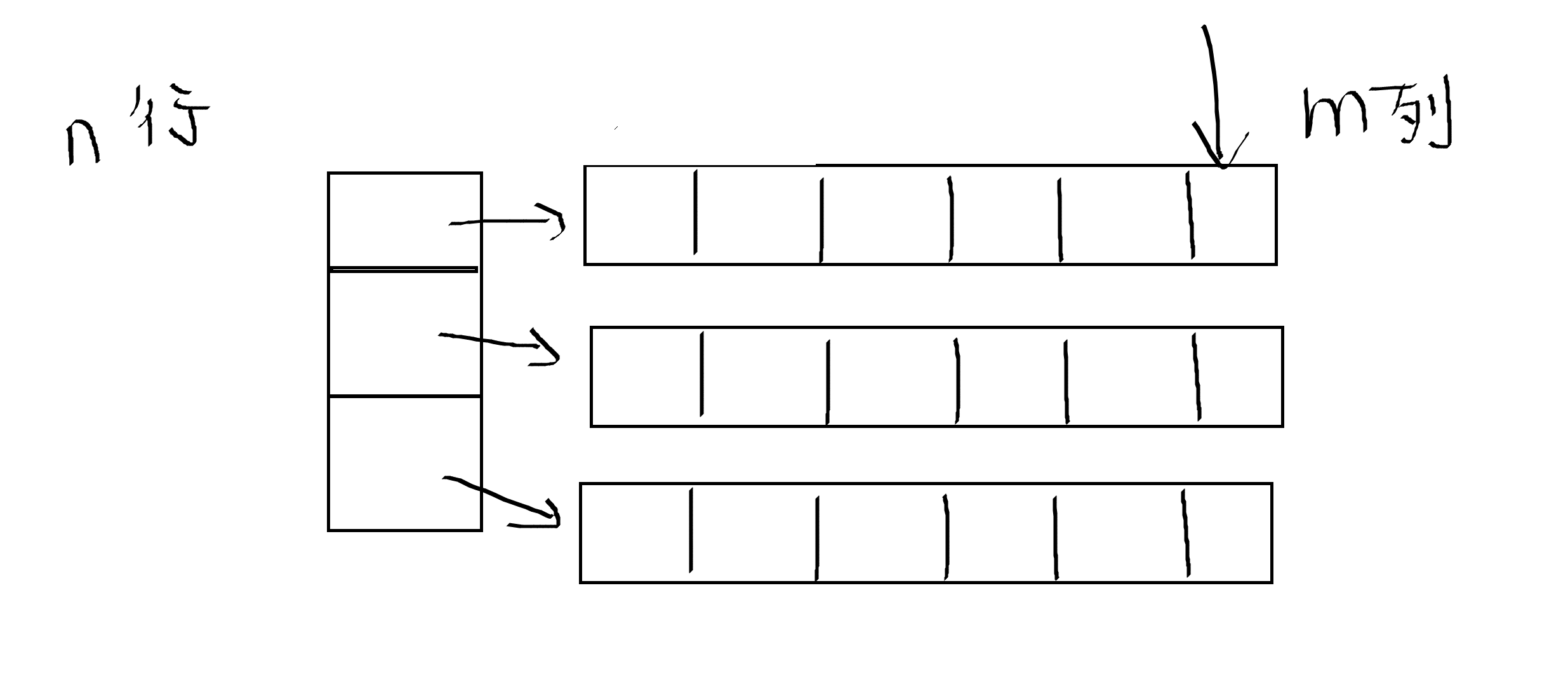
二位数组在内存空间的地址不一定是连续的:
外层数组(行)是连续的,但内层数组(列)可能不连续:
int[][] arr = new int[n][m]