有效的字母异位词

字符a到字符z的ASCII是26个连续的数值，所以字符a映射为下标0，相应的字符z映射为下标25。

那么任意字母和字母a相减的结果就是索引位置，在这个索引位置上计数，两个字符串分别对应计数的增cao操作和减操作，zhi'yao'zui只要最终遍历存储结果的数组，每一个位置是否为0即可

public boolean isAnagram(String s, String t) {
        int record[] = new int[26];//定义一个数组，长度为26，因为a~z是26个字母
        //分别遍历两个字符串，统计字母出现数量到record
        for (int i = 0; i < s.length(); i++){
            record[s.charAt(i) - 'a']++;
        }
        for (int i = 0; i < t.length(); i++) {
            record[t.charAt(i) - 'a']--;
        }
        //遍历record内如果数组内元素不为0，则说明字符不相等，返回false
        for (int i : record) {
            if (i != 0){
                return false;
            }
        }
        return true;
    }

两个数组的交集

思路一、数组

利用数组统计数字频率，动态检查交集并去重。

public int[] intersection(int[] nums1, int[] nums2) {
        // 假设数字范围是 0-1000（根据题目调整）
        int[] count = new int[1001]; // count[i] 表示数字 i 在 nums1 中出现的次数

        // 统计 nums1 的数字频率
        for (int num : nums1) {
            count[num]++;
        }

        // 检查 nums2 的数字是否在 nums1 中出现过
        List<Integer> resultList = new ArrayList<>();
        for (int target : nums2) {
            if (count[target] > 0) { // 如果 nums1 中有这个数字
                resultList.add(target); // 加入结果
                count[target] = 0; // 避免重复添加（题目要求结果去重）
            }
        }

        // 将 List 转为 int[]
        int[] result = new int[resultList.size()];
        for (int i = 0; i < resultList.size(); i++) {
            result[i] = resultList.get(i);
        }
        return result;
    }

思路二、HashSet

public int[] intersection(int[] nums1, int[] nums2) {
    if (nums1 == null || nums2 == null || nums1.length == 0 || nums2.length == 0) {
        return new int[0];
    }
    
    Set<Integer> set1 = new HashSet<>();
    Set<Integer> resSet = new HashSet<>();
    
    // 遍历数组1，存入set1
    for (int num : nums1) {
        set1.add(num);
    }
    
    // 遍历数组2，检查是否在set1中存在
    for (int num : nums2) {
        if (set1.contains(num)) {
            resSet.add(num);
        }
    }
    
    // 将结果转为数组
    int[] result = new int[resSet.size()];
    int index = 0;
    for (int num : resSet) {
        result[index++] = num;
    }
    return result;
}

快乐数

题意，平方和为1就是快乐数。

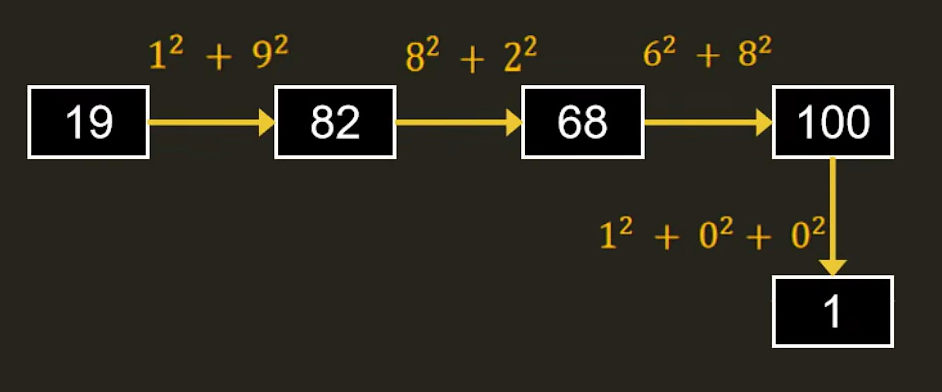
19 → 82 → 68 → 100 → 1（无重复，最终到 1，返回 true）

2之所以不是是因为，20的平方和等于4，形成环了

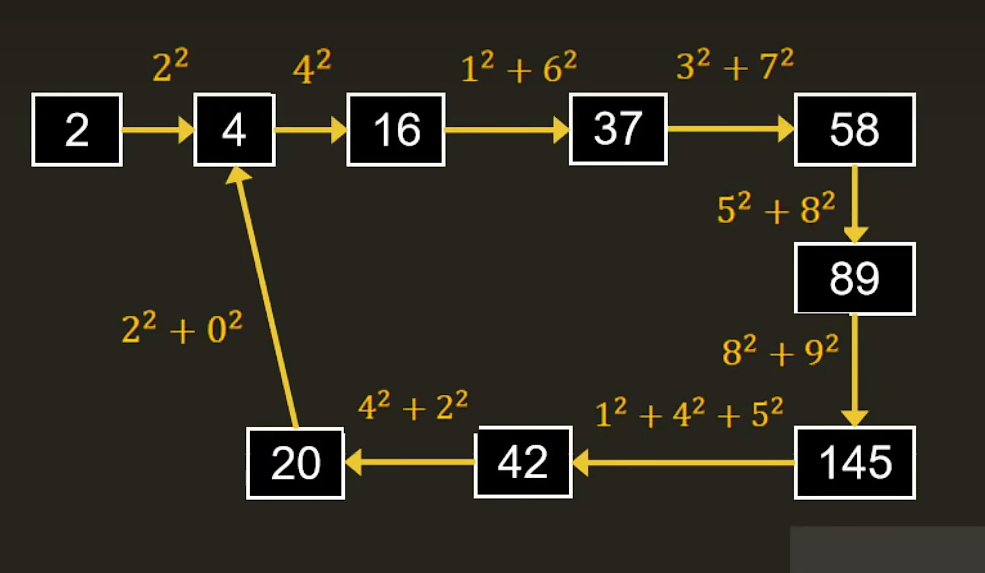
2 → 4 → 16 → 37 → 58 → 89 → 145 → 42 → 20 → 4（进入循环，返回 false）

public boolean isHappy(int n) {
    // 使用 HashSet 来记录已经出现过的数字，用于检测循环
    HashSet<Integer> seenNumbers = new HashSet<>();
    
    // 当 n 不等于 1 且没有进入循环时，继续计算
    while (n != 1 && !seenNumbers.contains(n)) {
        // 将当前数字加入已见集合，防止重复计算
        seenNumbers.add(n);
        // 计算下一个数字（各位数字的平方和）
        n = getNext(n);
    }
    
    // 如果最终 n 变成 1，则是快乐数；否则进入循环，不是快乐数
    return n == 1;
}

/**
 * 计算一个数的各位数字的平方和
 * 
 * @param n 输入的数字
 * @return 各位数字的平方和
 */
private int getNext(int n) {
    int sum = 0;
    while (n > 0) {
        // 取 n 的最后一位数字
        int digit = n % 10;
        // 将该数字的平方加到 sum 上
        sum += digit * digit;
        // 去掉 n 的最后一位（相当于 n / 10 取整）
        n = n / 10;
    }
    return sum;
}

两数之和

首先想到了遍历的办法，但是On^2

   public int[] twoSum(int[] nums, int target) {
        for (int i = 0; i < nums.length; i++) {
            for (int j = i + 1; j < nums.length; j++) {
                if (nums[i] + nums[j] == target) {
                    return new int[]{i,j};
                }
            }
        }
        //没有就返回null
        return null;
    }

另一种思路是，用map存放遍历过的元素，key是元素值，value是下标索引，如此时间复杂度On

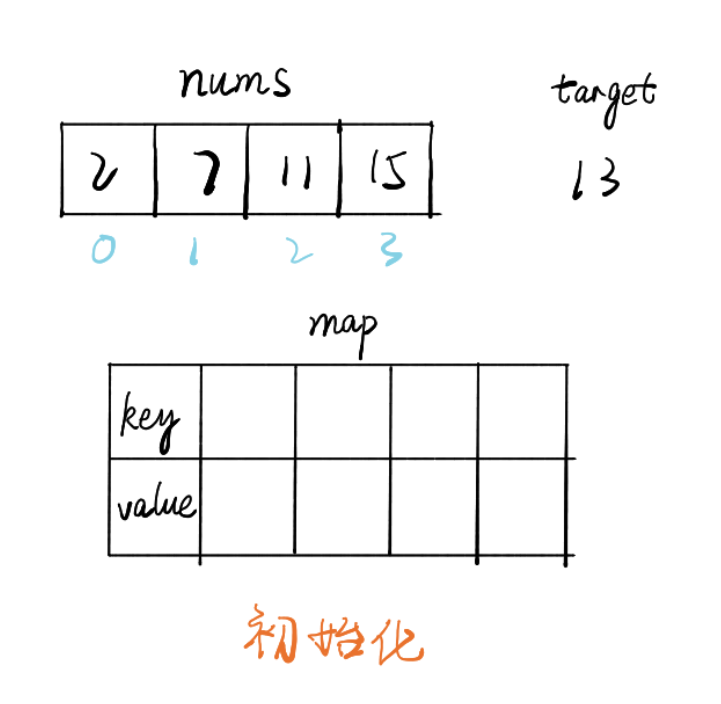
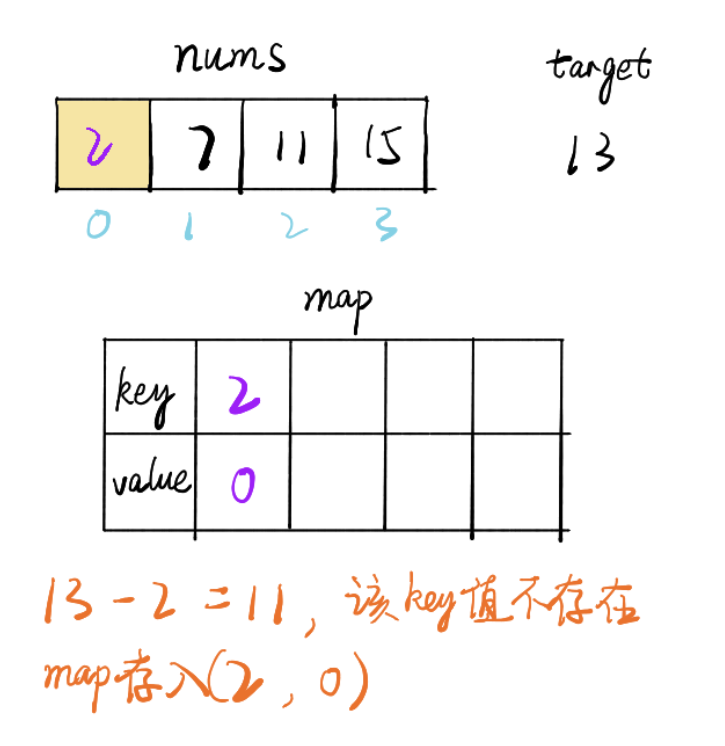
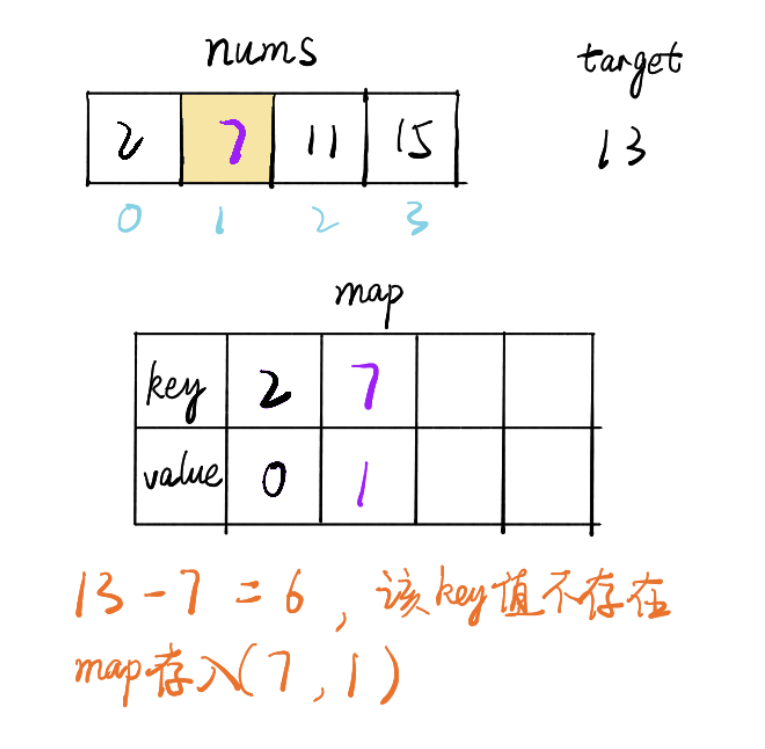
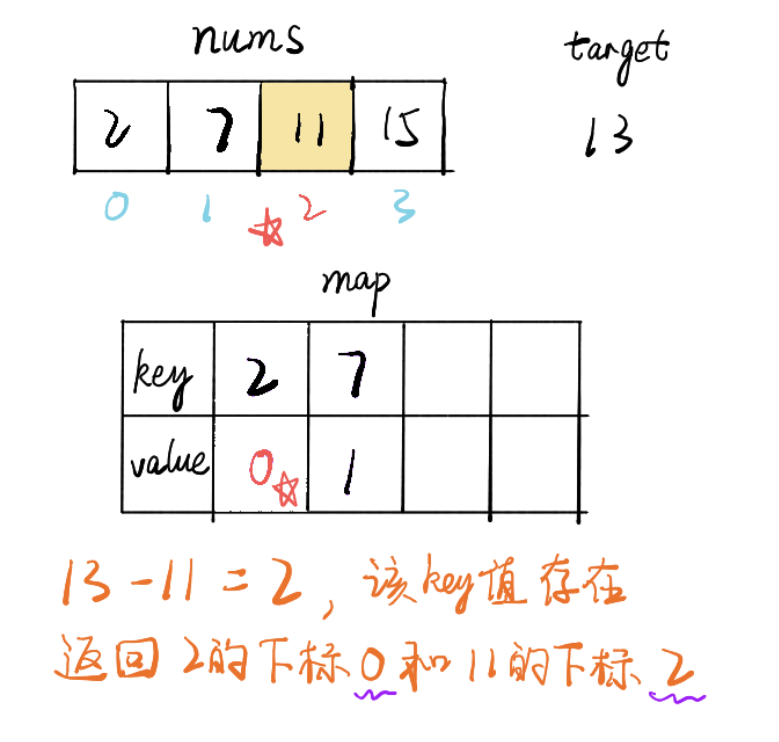
    public int[] twoSum(int[] nums, int target) {
        HashMap<Integer, Integer> result = new HashMap<>();
        for (int i = 0; i < nums.length; i++) {
            if (result.containsKey(target - nums[i])){
                //返回目标数的索引和当前数索引
                return new int[]{result.get(target - nums[i]), i};
            }
            //没有符合的数字，继续存入map中
            result.put(nums[i], i);
        }
        return null;
    }