四数相加

四数相加 II

HashMap 存一个数组，如 A。然后计算三个数组之和，如 BCD。时间复杂度为：O(n)+O(n^3)，得到 O(n^3).

HashMap 存三个数组之和，如 ABC。然后计算一个数组，如 D。时间复杂度为：O(n^3)+O(n)，得到 O(n^3).

HashMap存两个数组之和，如AB。然后计算两个数组之和，如 CD。时间复杂度为：O(n^2)+O(n^2)，得到 O(n^2).

我们以存 AB 两数组之和为例。首先求出 A 和 B 任意两数之和 sumAB，以 sumAB 为 key，sumAB 出现的次数为 value，存入 hashmap 中。

然后计算 C 和 D 中任意两数之和的相反数 sumCD，在 hashmap 中查找是否存在 key 为 sumCD。

    public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {
        HashMap<Integer, Integer> result = new HashMap<>();
        int count = 0;
        for (int i = 0; i < nums1.length; i++) {
            for (int j = 0; j < nums2.length; j++) {
                int sumAB = nums1[i] + nums2[j];
                if (result.containsKey(sumAB)) {
                    result.put(sumAB, result.get(sumAB) + 1);
                } else {
                    result.put(sumAB, 1);
                }
            }
        }

        for (int i = 0; i < nums3.length; i++) {
            for (int j = 0; j < nums4.length; j++) {
                int sumCD = nums3[i] + nums4[j];
                if (result.containsKey(-sumCD)) {
                    count += result.get(-sumCD);
                }
            }
        }
        return count;
    }

赎金信

赎金信

用一个长度为26的数组来记录magazine里字母出现的次数。

然后再用ransomNote 去验证这个数组是否包含了ransomNote 所需要的所有字母。

千万注意，magazine肯定是更长的，并且类似于字典，我们是统计他字母出现次数，后面需要的才能从里面减少

    public boolean canConstruct(String ransomNote, String magazine) {
        //题意条件 1 <= ransomNote.length, magazine.length <= 105
        if (ransomNote.length() > magazine.length()) {
            return false;
        }
        //不用map，因为空间开销大，用数组，储存a~z
        int[] record = new int[26];
        //遍历，统计字母出现次数
        for (int i = 0; i < magazine.length(); i++) {
            int index = magazine.charAt(i) - 'a';
            record[index] += 1;
        }
        for (int i = 0; i < ransomNote.length(); i++) {
            int index = ransomNote.charAt(i) - 'a';
            record[index] -= 1;
        }
        // 如果数组中存在负数，说明ransomNote字符串中存在magazine中没有的字符
        for (int i : record) {
            if (i < 0) {
                return false;
            }
        }
        return true;
    }

三数之和

转载自：三数之和（排序+双指针，易懂图解）

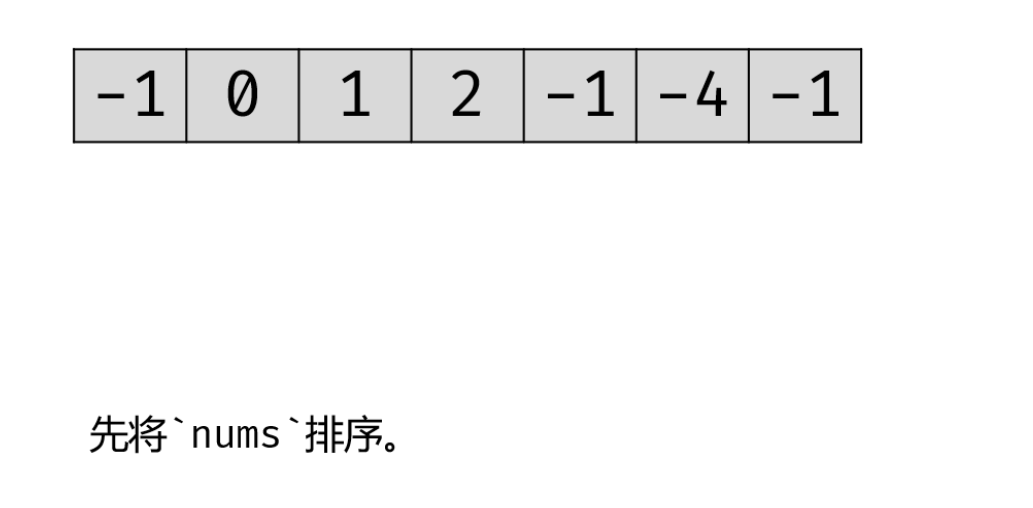
固定最小元素指针k，i和j两个指针取值范围在(k,nums.length)两端

要注意如果nums[k]>0，那么就不可能有结果直接结束即可。因为nums[j]>nums[i]>nums[k]

然后开始移动，需要注意去重，当k>0并且nums[k-1]==nums[k]的时候，保留nums[k]就可以了

总和是小于0的，所以i指针不断右移

继续右移，此时i和j相等了，所以不行。

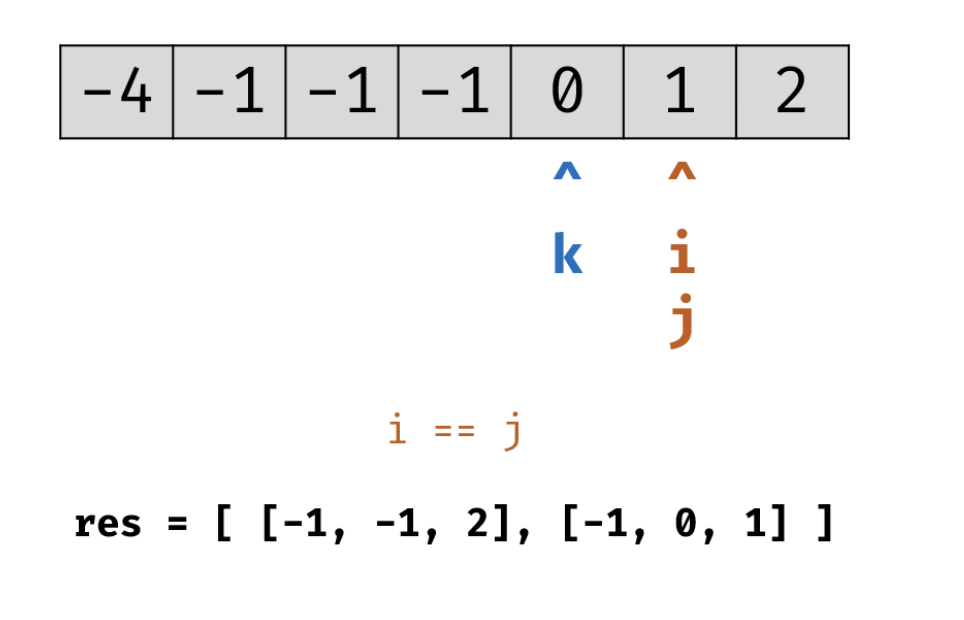
k右移，i重新回到k+1位置,j来到nums.length-1位置。

遇到重复的元素，跳过。此时和为0，记录k i j位置，然后跳过重复的元素，i右移，j左移

继续右移

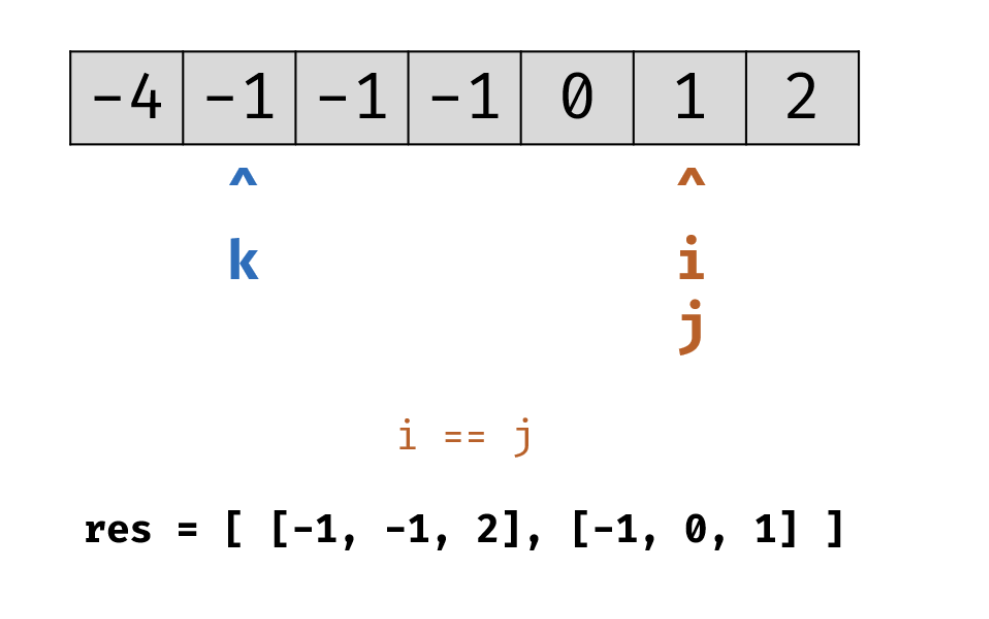
i和 j相等，不合题意，继续

总和大于0，j左移，此时i等于j

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        // 首先对数组进行排序，这是双指针法的前提条件
        Arrays.sort(nums);
        // 创建结果列表，用于存储所有满足条件的三元组
        List<List<Integer>> res = new ArrayList<>();
        
        // 外层循环，固定第一个数nums[k]
        for(int k = 0; k < nums.length - 2; k++){
            // 如果固定的第一个数已经大于0，由于数组已排序，后面的数都更大，不可能三数之和为0
            if(nums[k] > 0) break;
            
            // 跳过重复的第一个数，避免重复的三元组
            // 注意k>0的条件，避免数组越界
            if(k > 0 && nums[k] == nums[k - 1]) continue;
            
            // 设置双指针：i从k+1开始，j从数组末尾开始
            int i = k + 1, j = nums.length - 1;
            
            // 双指针遍历
            while(i < j){
                // 计算当前三个数的和
                int sum = nums[k] + nums[i] + nums[j];
                
                if(sum < 0){
                    // 和小于0，需要增大和，因此移动左指针i向右
                    // 使用while循环跳过重复的nums[i]
                    while(i < j && nums[i] == nums[++i]);
                } else if (sum > 0) {
                    // 和大于0，需要减小和，因此移动右指针j向左
                    // 使用while循环跳过重复的nums[j]
                    while(i < j && nums[j] == nums[--j]);
                } else {
                    // 找到满足条件的三元组，添加到结果列表
                    res.add(new ArrayList<Integer>(Arrays.asList(nums[k], nums[i], nums[j])));
                    
                    // 跳过重复的nums[i]和nums[j]，避免重复的三元组
                    while(i < j && nums[i] == nums[++i]);
                    while(i < j && nums[j] == nums[--j]);
                }
            }
        }
        // 返回所有满足条件的三元组
        return res;
    }
}