数据库-多表
在进行数据库表结构设计时,会根据业务需求及业务模块之间的关系,分析并设计表结构,由于业务之间相互关联,表结构之间也存在着各种联系,基本上分为三种:
一对多(多对一)
多对多
一对一
一对多
一对多关系实现:在数据库表中多的一方,添加字段,来关联属于一这方的主键。
外键约束
外键约束:让两张表的数据建立连接,保证数据的一致性和完整性。
对应的关键字:foreign key
-- 创建表时指定
create table 表名(
字段名 数据类型,
...
[constraint] [外键名称] foreign key (外键字段名) references 主表 (主表列名)
);
-- 建完表后,添加外键
alter table 表名 add constraint 外键名称 foreign key(外键字段名) references 主表(主表列名);物理外键和逻辑外键
物理外键
概念:使用foreign key定义外键关联另外一张表。
缺点:
影响增、删、改的效率(需要检查外键关系)。
仅用于单节点数据库,不适用与分布式、集群场景。
容易引发数据库的死锁问题,消耗性能。
逻辑外键
概念:在业务层逻辑中,解决外键关联。
通过逻辑外键,就可以很方便的解决上述问题。
在现在的企业开发中,很少会使用物理外键,都是使用逻辑外键。 甚至在一些数据库开发规范中,会明确指出禁止使用物理外键 foreign key
一对一
一对一关系表在实际开发中应用起来比较简单,通常是用来做单表的拆分,也就是将一张大表拆分成两张小表,将大表中的一些基础字段放在一张表当中,将其他的字段放在另外一张表当中,以此来提高数据的操作效率。
一对一的应用场景: 用户表(基本信息+身份信息)

- 基本信息:用户的ID、姓名、性别、手机号、学历
- 身份信息:民族、生日、身份证号、身份证签发机关,身份证的有效期(开始时间、结束时间)
如果在业务系统当中,对用户的基本信息查询频率特别的高,但是对于用户的身份信息查询频率很低,此时出于提高查询效率的考虑,我就可以将这张大表拆分成两张小表,第一张表存放的是用户的基本信息,而第二张表存放的就是用户的身份信息。他们两者之间一对一的关系,一个用户只能对应一个身份证,而一个身份证也只能关联一个用户。
-- 用户身份信息表
create table tb_user_card(
id int unsigned primary key auto_increment comment 'ID',
nationality varchar(10) not null comment '民族',
birthday date not null comment '生日',
idcard char(18) not null comment '身份证号',
issued varchar(20) not null comment '签发机关',
expire_begin date not null comment '有效期限-开始',
expire_end date comment '有效期限-结束',
user_id int unsigned not null unique comment '用户ID',
constraint fk_user_id foreign key (user_id) references tb_user(id)
) comment '用户身份信息表';一对一 :在任意一方加入外键,关联另外一方的主键,并且设置外键为唯一的(UNIQUE)
多对多
多对多的关系在开发中属于也比较常见的。比如:学生和老师的关系,一个学生可以有多个授课老师,一个授课老师也可以有多个学生。在比如:学生和课程的关系,一个学生可以选修多门课程,一个课程也可以供多个学生选修。
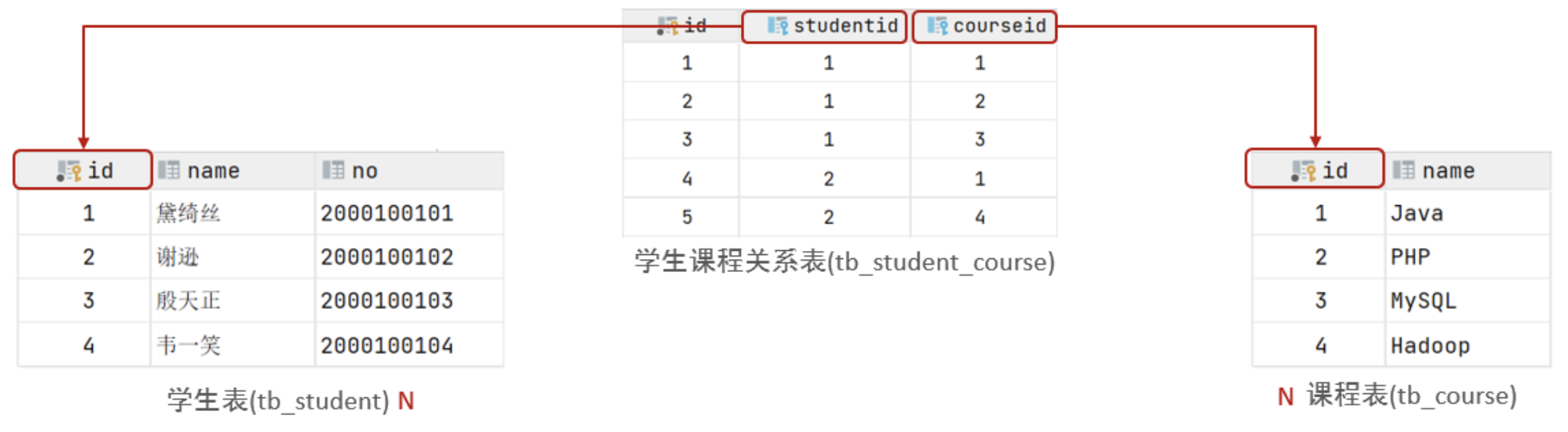
案例:学生与课程的关系
关系:一个学生可以选修多门课程,一门课程也可以供多个学生选择
实现关系:建立第三张中间表,中间表至少包含两个外键,分别关联两方主键
-- 学生表
create table tb_student(
id int auto_increment primary key comment '主键ID',
name varchar(10) comment '姓名',
no varchar(10) comment '学号'
) comment '学生表';
-- 课程表
create table tb_course(
id int auto_increment primary key comment '主键ID',
name varchar(10) comment '课程名称'
) comment '课程表';
-- 学生课程表(中间表)
create table tb_student_course(
id int auto_increment comment '主键' primary key,
student_id int not null comment '学生ID',
course_id int not null comment '课程ID',
constraint fk_courseid foreign key (course_id) references tb_course (id),
constraint fk_studentid foreign key (student_id) references tb_student (id)
)comment '学生课程中间表';多表查询
多表查询:查询时从多张表中获取所需数据
单表查询的SQL语句:select 字段列表 from 表名;
那么要执行多表查询,只需要使用逗号分隔多张表即可,如: select 字段列表 from 表1, 表2;
笛卡尔积:笛卡尔乘积是指在数学中,两个集合(A集合和B集合)的所有组合情况。
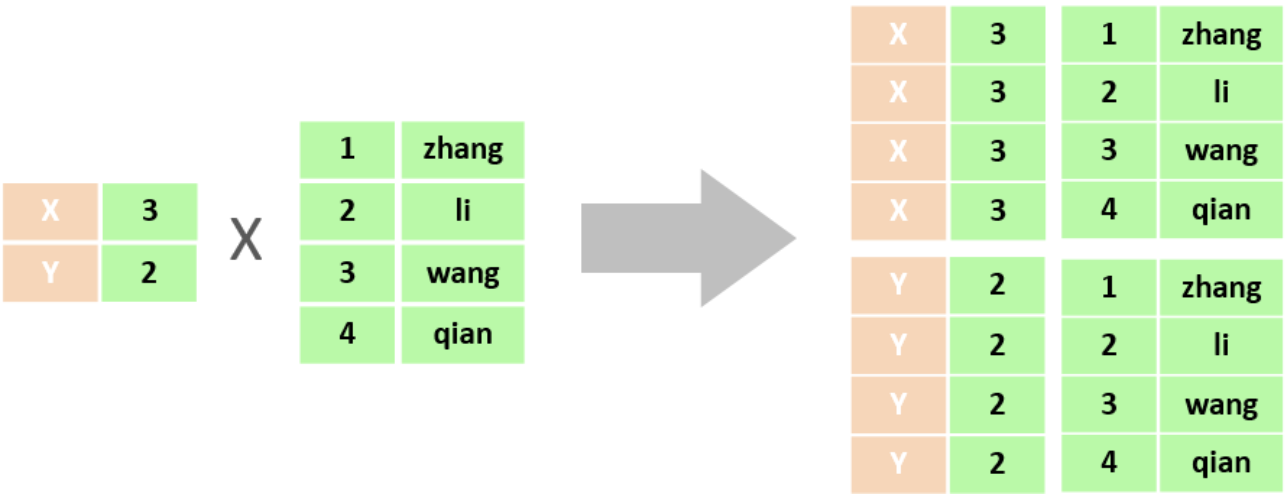
在多表查询时,需要消除无效的笛卡尔积,只保留表关联部分的数据
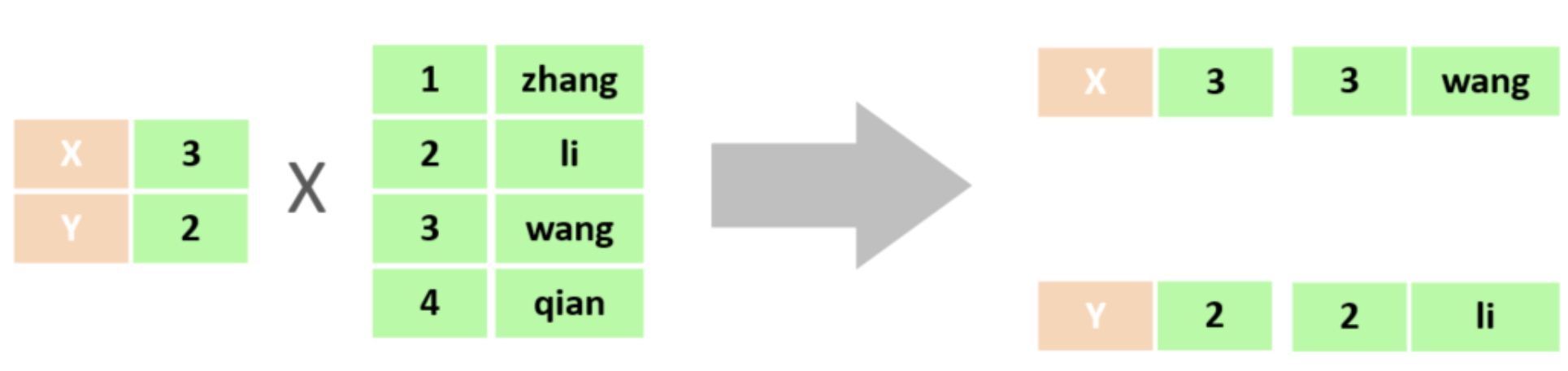
在SQL语句中,如何去除无效的笛卡尔积呢?只需要给多表查询加上连接查询的条件即可。
select * from tb_emp , tb_dept where tb_emp.dept_id = tb_dept.id ;分类
多表查询可以分为:
连接查询
内连接:相当于查询A、B交集部分数据
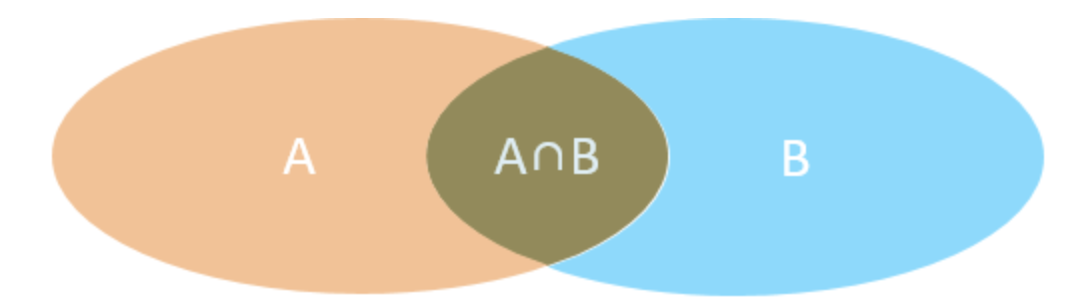
外连接
左外连接:查询左表所有数据(包括两张表交集部分数据)
右外连接:查询右表所有数据(包括两张表交集部分数据)
子查询
内连接
内连接查询:查询两表或多表中交集部分数据。
内连接从语法上可以分为:
隐式内连接
显式内连接
隐式内连接语法:
select 字段列表 from 表1 , 表2 where 条件 ... ;显式内连接语法:
select 字段列表 from 表1 [ inner ] join 表2 on 连接条件 ... ;
外连接
外连接分为两种:左外连接 和 右外连接。
左外连接语法结构:
select 字段列表 from 表1 left [ outer ] join 表2 on 连接条件 ... ;左外连接相当于查询表1(左表)的所有数据,当然也包含表1和表2交集部分的数据。
右外连接语法结构:
select 字段列表 from 表1 right [ outer ] join 表2 on 连接条件 ... ;右外连接相当于查询表2(右表)的所有数据,当然也包含表1和表2交集部分的数据。
示例
-- 左外连接:以left join关键字左边的表为主表,查询主表中所有数据,以及和主表匹配的右边表中的数据(小表驱动大表)
select emp.name , dept.name
from tb_emp AS emp left join tb_dept AS dept
on emp.dept_id = dept.id;尽量用 LEFT JOIN 替代 RIGHT JOIN,因为 MySQL 对 LEFT JOIN 优化更好,且更符合开发习惯。
子查询
SQL语句中嵌套select语句,称为嵌套查询,又称子查询。
SELECT * FROM t1 WHERE column1 = ( SELECT column1 FROM t2 ... );子查询外部的语句可以是insert / update / delete / select 的任何一个,最常见的是 select。
根据子查询结果的不同分为:
标量子查询(子查询结果为单个值[一行一列])
列子查询(子查询结果为一列,但可以是多行)
行子查询(子查询结果为一行,但可以是多列)
表子查询(子查询结果为多行多列[相当于子查询结果是一张表])
子查询可以书写的位置:
where之后
from之后
select之后
标量子查询
子查询返回的结果是单个值(数字、字符串、日期等),最简单的形式,这种子查询称为标量子查询。
常用的操作符: = <> > >= < <=
-- 1.查询"教研部"部门ID
select id from tb_dept where name = '教研部'; #查询结果:2
-- 2.根据"教研部"部门ID, 查询员工信息
select * from tb_emp where dept_id = 2;
-- 合并出上两条SQL语句
select * from tb_emp where dept_id = (select id from tb_dept where name = '教研部');列子查询
子查询返回的结果是一列(可以是多行),这种子查询称为列子查询。
常用的操作符:
-- 1.查询"销售部"和"市场部"的部门ID
select id from tb_dept where name = '教研部' or name = '咨询部'; #查询结果:3,2
-- 1.1 IN 的替代写法)
SELECT id FROM tb_dept WHERE name IN ('教研部', '咨询部');
-- 2.根据部门ID, 查询员工信息
select * from tb_emp where dept_id in (3,2);
-- 合并以上两条SQL语句
select * from tb_emp where dept_id in (select id from tb_dept where name = '教研部' or name = '咨询部');行子查询
子查询返回的结果是一行(可以是多列),这种子查询称为行子查询。
常用的操作符:= 、<> 、IN 、NOT IN
案例:查询与"韦一笑"的入职日期及职位都相同的员工信息
可以拆解为两步进行:
查询 "韦一笑" 的入职日期 及 职位
查询与"韦一笑"的入职日期及职位相同的员工信息
-- 查询"韦一笑"的入职日期 及 职位
select entrydate , job from tb_emp where name = '韦一笑'; #查询结果: 2007-01-01 , 2
-- 查询与"韦一笑"的入职日期及职位相同的员工信息
select * from tb_emp where (entrydate,job) = ('2007-01-01',2);
-- 合并以上两条SQL语句
select * from tb_emp where (entrydate,job) = (select entrydate , job from tb_emp where name = '韦一笑');表子查询
子查询返回的结果是多行多列,常作为临时表,这种子查询称为表子查询。
select * from emp where entrydate > '2006-01-01';
select e.*, d.* from (select * from emp where entrydate > '2006-01-01') e 左外查询以e表为主表
left join dept d
on e.dept_id = d.id ;事务
事务是一组操作的集合,它是一个不可分割的工作单位。事务会把所有的操作作为一个整体一起向系统提交或撤销操作请求,即这些操作要么同时成功,要么同时失败。
MYSQL中有两种方式进行事务的操作:
自动提交事务:即执行一条sql语句提交一次事务。(默认MySQL的事务是自动提交)
手动提交事务:先开启,再提交
事务操作有关的SQL语句:
手动提交事务使用步骤:
第1种情况:开启事务 => 执行SQL语句 => 成功 => 提交事务
第2种情况:开启事务 => 执行SQL语句 => 失败 => 回滚事务
-- 开启事务
start transaction ;
-- 删除学工部
delete from tb_dept where id = 1;
-- 删除学工部的员工
delete from tb_emp where dept_id = 1;
-- 提交事务 (成功时执行)
commit ;
-- 回滚事务 (出错时执行)
rollback ;面试题:事务有哪些特性?
原子性(Atomicity) :原子性是指事务包装的一组sql是一个不可分割的工作单元,事务中的操作要么全部成功,要么全部失败。
一致性(Consistency):一个事务完成之后数据都必须处于一致性状态。
如果事务成功的完成,那么数据库的所有变化将生效。
如果事务执行出现错误,那么数据库的所有变化将会被回滚(撤销),返回到原始状态。
隔离性(Isolation):多个用户并发的访问数据库时,一个用户的事务不能被其他用户的事务干扰,多个并发的事务之间要相互隔离。
一个事务的成功或者失败对于其他的事务是没有影响。
持久性(Durability):一个事务一旦被提交或回滚,它对数据库的改变将是永久性的,哪怕数据库发生异常,重启之后数据亦然存在。
索引
索引(index):是帮助数据库高效获取数据的数据结构 。
简单来讲,就是使用索引可以提高查询的效率。
结构
MySQL数据库支持的索引结构有很多,如:Hash索引、B+Tree索引、Full-Text索引等。
我们平常所说的索引,如果没有特别指明,都是指默认的 B+Tree 结构组织的索引。
二叉查找树:左边的子节点比父节点小,右边的子节点比父节点大
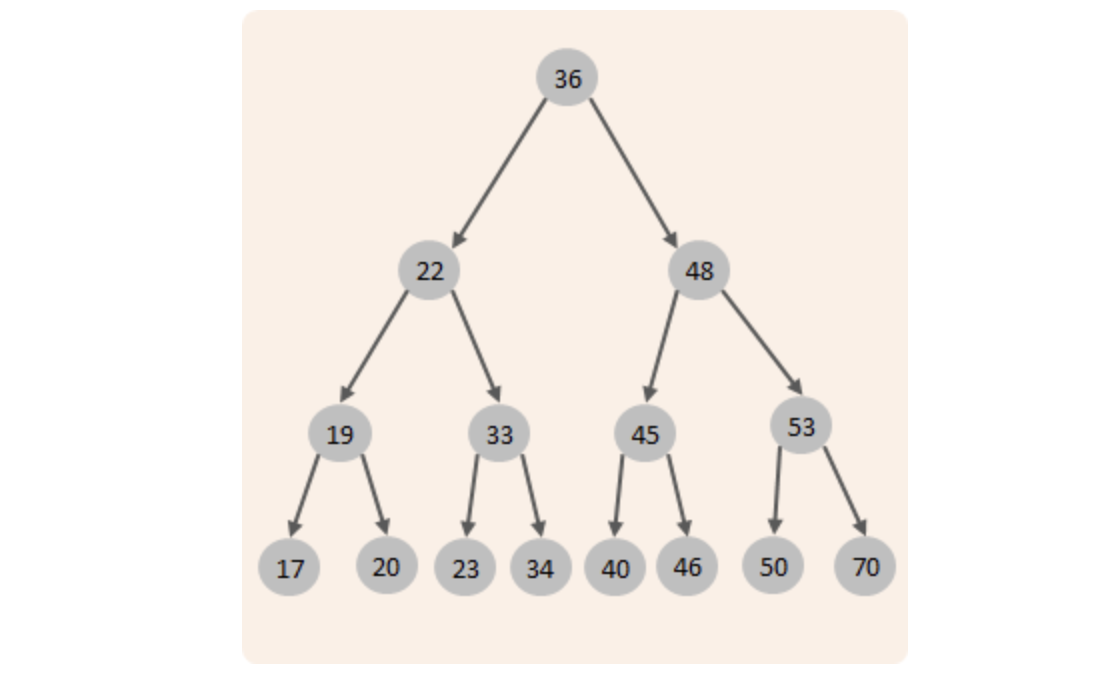
当我们向二叉查找树保存数据时,是按照从大到小(或从小到大)的顺序保存的,此时就会形成一个单向链表,搜索性能会打折扣。

可以选择平衡二叉树或者是红黑树来解决上述问题。(红黑树也是一棵平衡的二叉树)
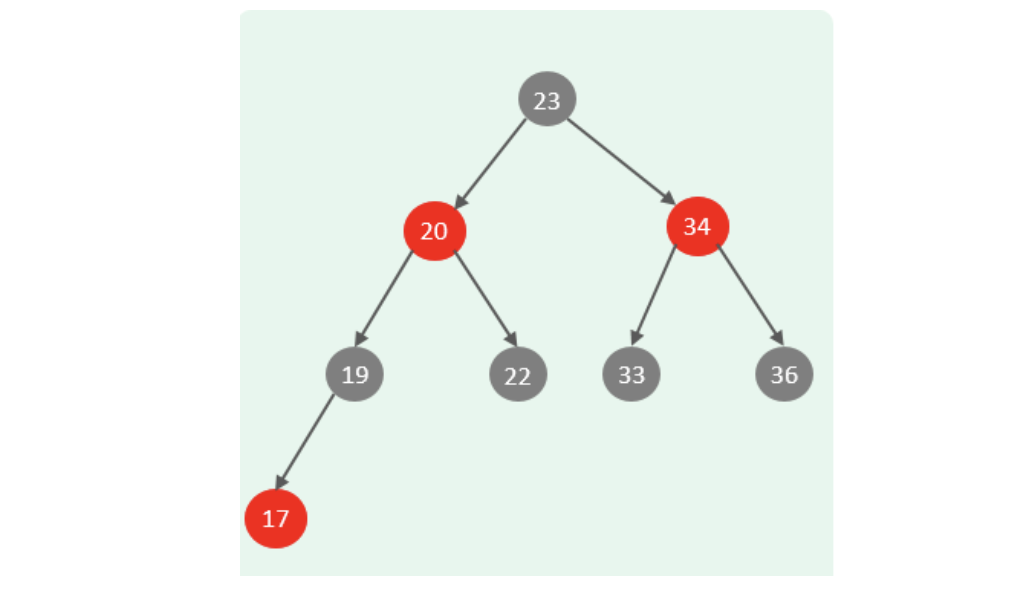
是在Mysql数据库中并没有使用二叉搜索数或二叉平衡数或红黑树来作为索引的结构。
思考:采用二叉搜索树或者是红黑树来作为索引的结构有什么问题?
最大的问题就是在数据量大的情况下,树的层级比较深,会影响检索速度。因为不管是二叉搜索数还是红黑数,一个节点下面只能有两个子节点。此时在数据量大的情况下,就会造成数的高度比较高,树的高度一旦高了,检索速度就会降低。
说明:如果数据结构是红黑树,那么查询1000万条数据,根据计算树的高度大概是23左右,这样确实比之前的方式快了很多,但是如果高并发访问,那么一个用户有可能需要23次磁盘IO,那么100万用户,那么会造成效率极其低下。所以为了减少红黑树的高度,那么就得增加树的宽度,就是不再像红黑树一样每个节点只能保存一个数据,可以引入另外一种数据结构,一个节点可以保存多个数据,这样宽度就会增加从而降低树的高度。这种数据结构例如BTree就满足。
B+Tree(多路平衡搜索树)结构中如何避免这个问题:
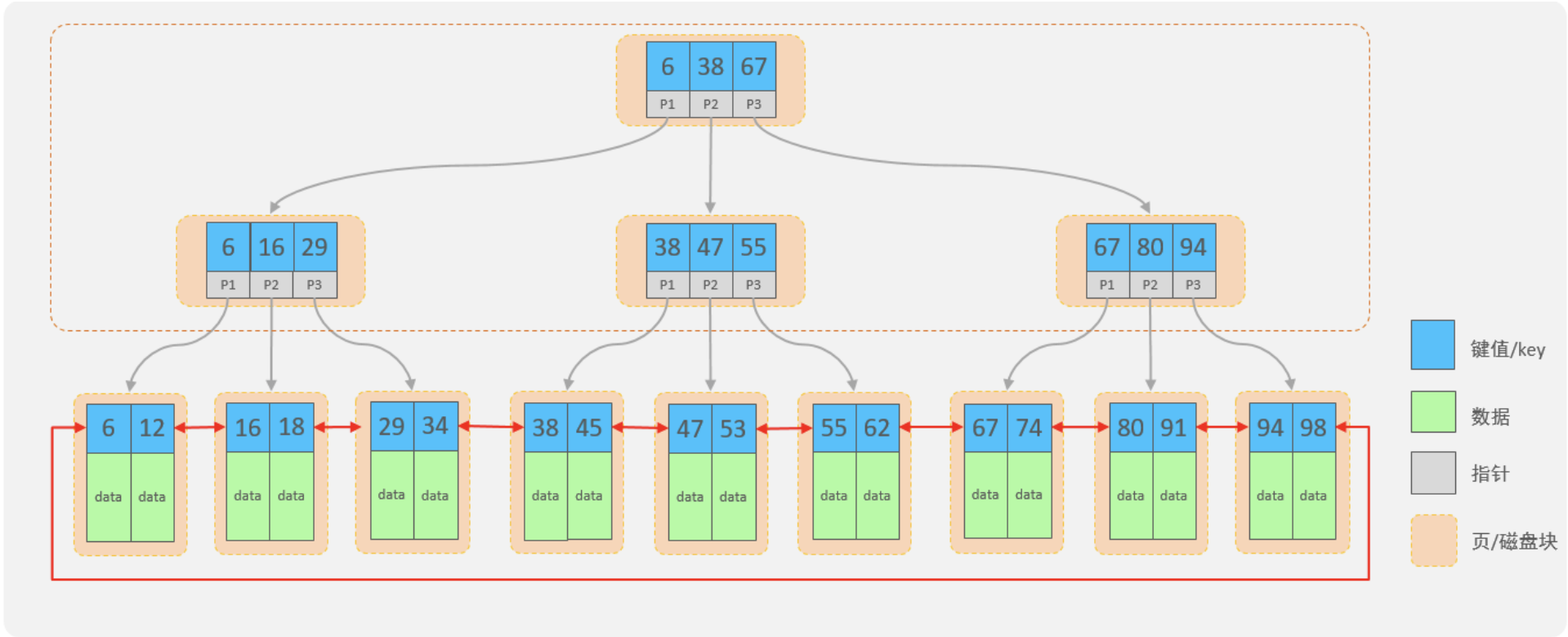
B+Tree结构:
每一个节点,可以存储多个key(有n个key,就有n个指针)
节点分为:叶子节点、非叶子节点
叶子节点,就是最后一层子节点,所有的数据都存储在叶子节点上
非叶子节点,不是树结构最下面的节点,用于索引数据,存储的的是:key+指针
为了提高范围查询效率,叶子节点形成了一个双向链表,便于数据的排序及区间范围查询
拓展:非叶子节点都是由key+指针域组成的,一个key占8字节,一个指针占6字节,而一个节点总共容量是16KB,那么可以计算出一个节点可以存储的元素个数:16*1024字节 / (8+6)=1170个元素。
查看mysql索引节点大小:show global status like 'innodb_page_size'; -- 节点大小:16384
当根节点中可以存储1170个元素,那么根据每个元素的地址值又会找到下面的子节点,每个子节点也会存储1170个元素,那么第二层即第二次IO的时候就会找到数据大概是:1170*1170=135W。也就是说B+Tree数据结构中只需要经历两次磁盘IO就可以找到135W条数据。
对于第二层每个元素有指针,那么会找到第三层,第三层由key+数据组成,假设key+数据总大小是1KB,而每个节点一共能存储16KB,所以一个第三层一个节点大概可以存储16个元素(即16条记录)。那么结合第二层每个元素通过指针域找到第三层的节点,第二层一共是135W个元素,那么第三层总元素大小就是:135W*16结果就是2000W+的元素个数。
结合上述分析B+Tree有如下优点:
千万条数据,B+Tree可以控制在小于等于3的高度
所有的数据都存储在叶子节点上,并且底层已经实现了按照索引进行排序,还可以支持范围查询,叶子节点是一个双向链表,支持从小到大或者从大到小查找
语法
创建索引
create [ unique ] index 索引名 on 表名 (字段名,... ) ;
-- 示例:为tb_emp表的name字段建立一个索引
create index idx_emp_name on tb_emp(name);在创建表时,如果添加了主键和唯一约束,就会默认创建:主键索引、唯一约束

删除索引
drop index 索引名 on 表名;
-- 案例:删除 tb_emp 表中name字段的索引
drop index idx_emp_name on tb_emp;注意事项:
主键字段,在建表时,会自动创建主键索引
添加唯一约束时,数据库实际上会添加唯一索引